Plongement de Kuratowski - Math'φsics

Plongement de Kuratowski

Formulaire de report
Problème d'affichage Contenu de la note peu pertinent
Théorème de Kuratowski-Wojdysławski :
\((E,d)\) est un Espace métrique

$$\Huge\iff$$

il existe un espace métrique complet qui admet un sous-espace dense s'identifiant isométriquement à \(E\)

cette isométrie est $$i:\begin{align} E&\longrightarrow\mathcal C_b(E)\\ x&\longmapsto i_x:\begin{aligned}E&\longrightarrow{\Bbb R}\\ y&\longmapsto d(x,y)-d(a,y)\end{aligned}\end{align}$$avec \(a\in E\) quelconque

cet espace est unique à isométrie bijective près
Exercices

Plongement de Kuratowski (existence) Montrer que \(i_x\in\mathcal C_b(E)\).

Continuité via la continuité de la distance.

Borne obtenue par inégalité triangulaire.

Plongement de Kuratowski (existence) Montrer qu'il existe un espace complet \(\hat E\) dans lequel \(i(E)\) est dense.

Candidat \(\overline{i(E)}\).

Il est fermé, donc complet dans l'espace métrique complet.

Et on a la densité par définition (avec l'adhérence).

Plongement de Kuratowski (unicité) Soient \(F_1,F_2\) deux espaces métriques complets et \(j_
Les isométries sont injectives, donc on peut poser des réciproques en restreignant à \(j_i(E)\).
E\to F_1\) et \(j_
On peut vérifier facilement que ce sont des isométries puisque les \(j_i\) le sont.
E\to F_2\) deux isométries tq \(j_1(E)\) est dense dans \(F_1\) et \(j_2(E)\) est dense dans \(F_2\).
Construire une isométrie bijective de \(F_1\) dans \(F_2\).
1:

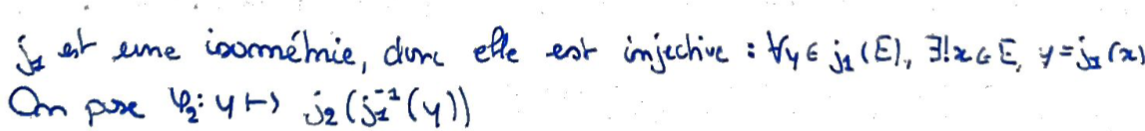
2:

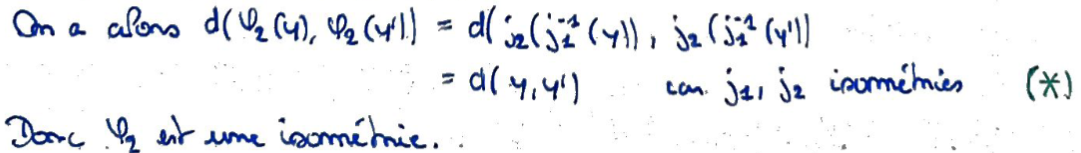
On utilise un Prolongement d'une fonction uniformément continue pour étendre la fonction à tout \(F_i\).

C'est toujours une isométrie par continuité.

On peut construire l'autre fonction de la même manière, ce qui montre que l'isométrie est bijective.